正态分布的发展

高斯正态分布是现代数学中一个至关重要的概念。早在18世纪，人们已经开始研究随机变量的性质，但直到19世纪末，这一概念才被高斯细致地研究和发展。

高斯对正态分布做出了最初的贡献，他深入研究了误差的传播和测量理论，并意识到许多物理现象可以用正态分布来描述。他提出的中心极限定理指出，大量独立同分布的随机变量的平均值服从正态分布，而这一定理则为后来统计学的发展奠定了基础。此后，人们开始广泛研究正态分布的性质和应用，并不断将这一概念拓展到各个领域。

正态分布在统计学、自然科学和社会科学中都有着重要的应用。在统计学中，正态分布广泛应用于样本均值和总体均值的推断、假设检验和置信区间的构造等方面，在自然科学中，正态分布则被用于分析实验数据、测量误差和模拟随机现象等，在社会科学中，正态分布则可以用于研究人口、经济和金融等领域的问题。

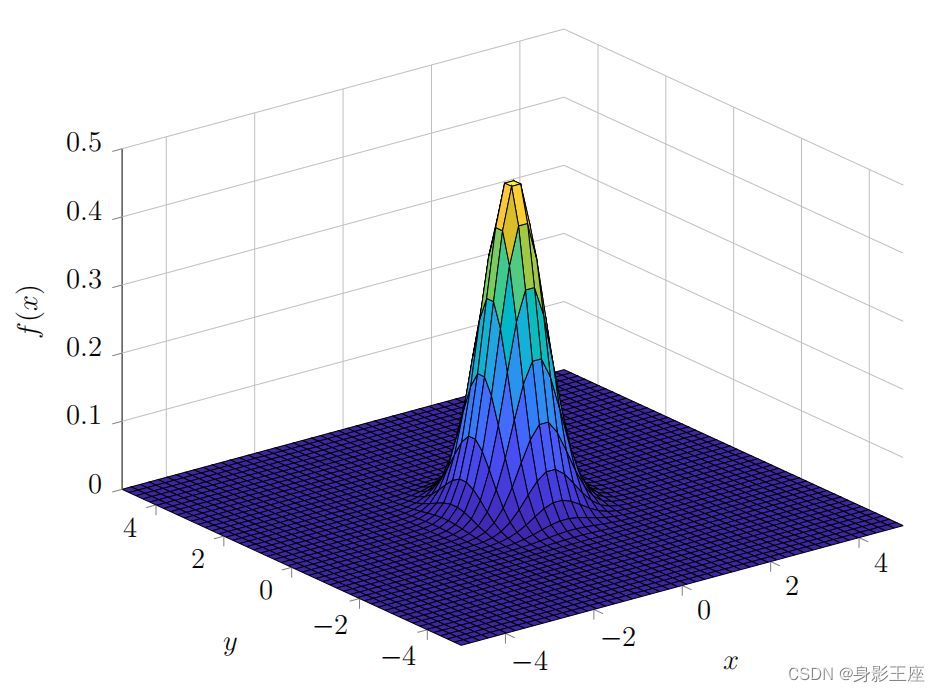
正态分布的研究历程和广泛应用，反映出数学在社会发展中所起到的巨大作用。数学不仅带给人们更多的技术利器，还教给人们思考和创新的方法，推动了科学技术的发展，为人类社会进步做出了重要贡献。正如高斯所说：“数学是天才的花环，是科学理性与人文情感融为一体的产物。”

应用场景

正态分布是现代数学中的一个核心概念，其广泛的应用涉及到统计学、自然科学和社会科学等多个领域。以下是一些正态分布的具体应用场景：

1. 质量控制和生产过程控制

在工业制造业中，生产过程中的误差和变异性可能会影响产品的质量。为了控制这些误差，人们常常采用正态分布来描述产品特性的变化范围，并建立质量控制图来监测生产过程的状态。例如，汽车制造厂商通常会对发动机输出功率进行检测，而这些数据的分布往往符合正态分布。

2. 计算股票和期权的风险价值

在金融领域中，正态分布被广泛应用于计算股票和期权的风险价值。人们假设股票价格和期权价格服从正态分布，通过计算标准差和期望值等参数，可以得出各种风险指标，如价值-at-风险（VaR）和期望损失（Expected shortfall）等，从而帮助投资者对风险进行评估和管理。

3. 研究人体各种指标的正常范围

在医学研究中，正态分布被用于研究人体各种指标的正常范围。例如，人体身高和体重的分布往往符合正态分布，通过计算平均值和标准差等参数，可以得出这些指标的正常范围，帮助医学工作者进行诊断和治疗。

4. 分析实验数据

在自然科学研究中，正态分布则被用于分析实验数据，如研究材料的力学性能、测量光学信号等。通过正态分布进行拟合和计算，可以得到实验数据的分布规律和相关参数，从而更好地理解实验现象。

5. 研究人口、经济和金融等领域的问题

在社会科学中，正态分布也有着广泛应用。例如，在人口统计学中，人们常常使用正态分布来研究人口特征的分布规律和变化趋势；在经济学中，正态分布则被用于建立金融市场模型和对经济指标进行预测；在金融学中，正态分布则是期权定价模型的基础，可用于评估衍生证券的风险和收益。

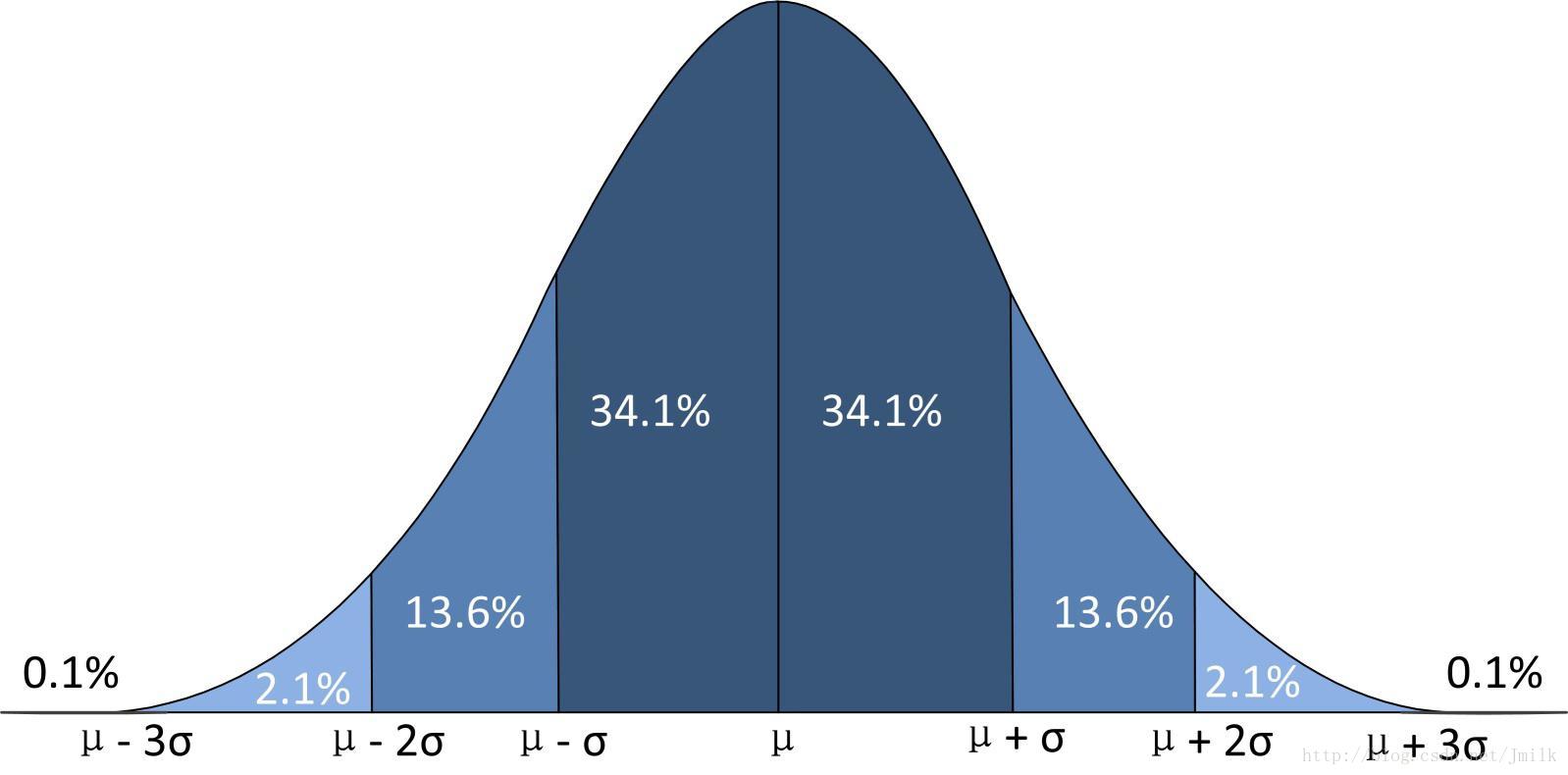
总之，正态分布在各个领域中都有着广泛的应用，其研究和拓展也为相关学科的发展做出了巨大贡献。

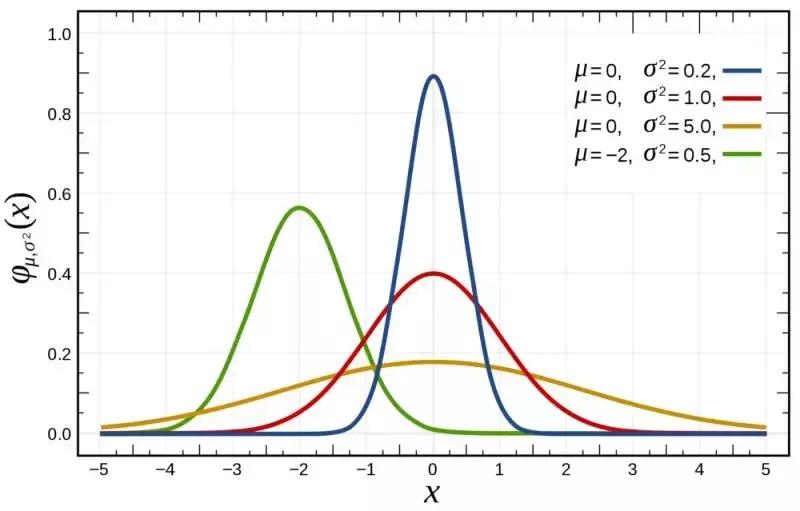
正态分布，又称高斯分布，可用于描述一组随机变量的概率分布。正态分布可以由以下一维连续概率密度函数表示：

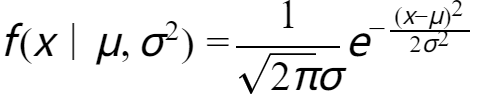
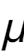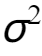其中， 和 分别表示分布的均值和方差。概率密度函数图形呈钟形曲线，在均值处取得最大值，两侧逐渐趋近于0。如果 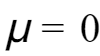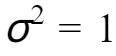，，则该分布称为标准正态分布。

正态分布的数学推导过程

假设 X 是一个一维连续随机变量，其概率密度函数为 f(x)。我们希望找到一个分布可以描述 X 的特点。

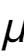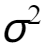首先，定义该分布的期望 和方差 为：

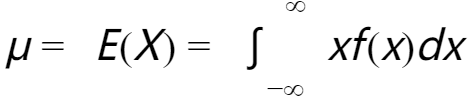
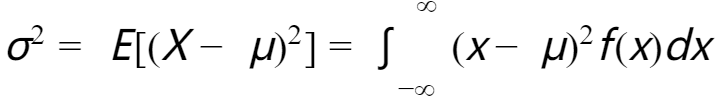
接下来，将 X 转换成标准正态分布 Z，即 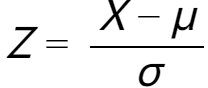，此时有：

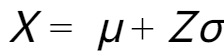
然后，我们可以利用 $Z$ 的分布特性来推导 $X$ 的概率密度函数。由于 $Z$ 的方差为1，我们有：

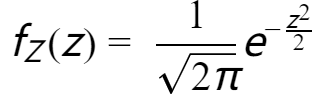
根据全概率公式，可以得到 $X$ 的概率密度函数为：

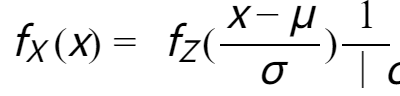
其中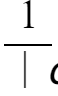，是为了保证概率密度函数的积分为1。

将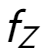代入上式，可得：

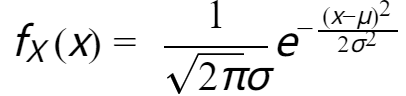
这就是正态分布的概率密度函数。正态分布的期望为 ，方差为 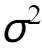，标准正态分布的期望为0，方差为1。

正态分布的数学推导过程比较复杂，但是其结果简明清晰，非常符合实际情况，因此在各个领域都有着广泛的应用。